The transistor, invented in the early 1950s, revolutionized the field of electronics. Replacing the vacuum tube as an amplifying device, it soon became the fundamental building block for modern electronics. By definition, a transistor is a semiconductor device that can be used to control current flow. Advantages of transistors include extremely long life, minimal power and voltage requirements, small physical size, and rugged construction that lends well to vibration resistance.

The bipolar transistor evolved from a single packaged device into many transistors imbedded on a single integrated chip. Bipolar transistors, also called bipolar junction transistors or BJTs, are three-terminal devices that can function as electronic switches or signal amplifiers. The BJT is widely used in discrete circuits as well as in analog and digital integrated circuits, or ICs.
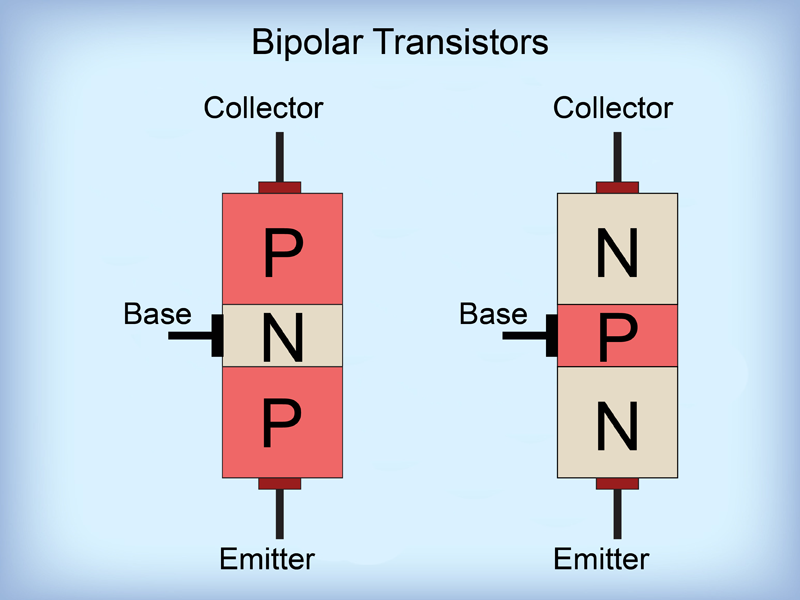
This figure shows a simplified structure for a BJT. The BJT consists of three semiconductor regions: the emitter region, the base region, and the collector region. BJTs are classified as either NPN or PNP according to the arrangement of their N-type and P-type materials.
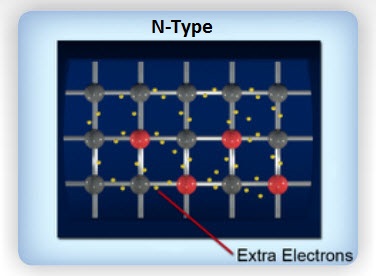
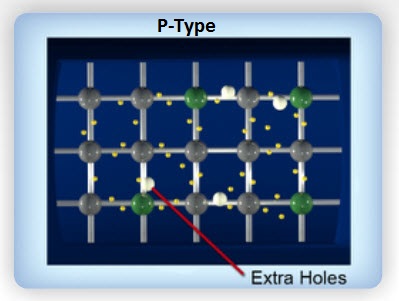
N-Type/P-Type Material – A semiconductor material doped with small amounts of an element with extra electrons is called N-type material. It has extra negatively charged particles, or free electrons, that can move freely from negatively charged areas to positively charged areas. On the other hand, a semiconductor material doped with small amounts of an element that creates extra holes is called P-type material. Since it has extra positively charged particles, it allows electrons to move from hole to hole.
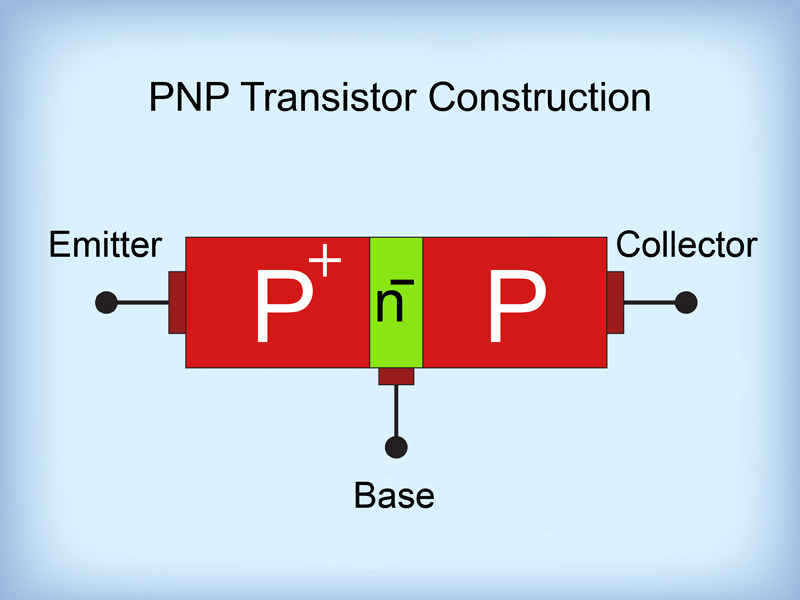
PNP Transistors
This diagram shows the construction of a PNP transistor. As you can see, an N-type silicon (the green layer) is sandwiched between two P-type materials (the red layers).
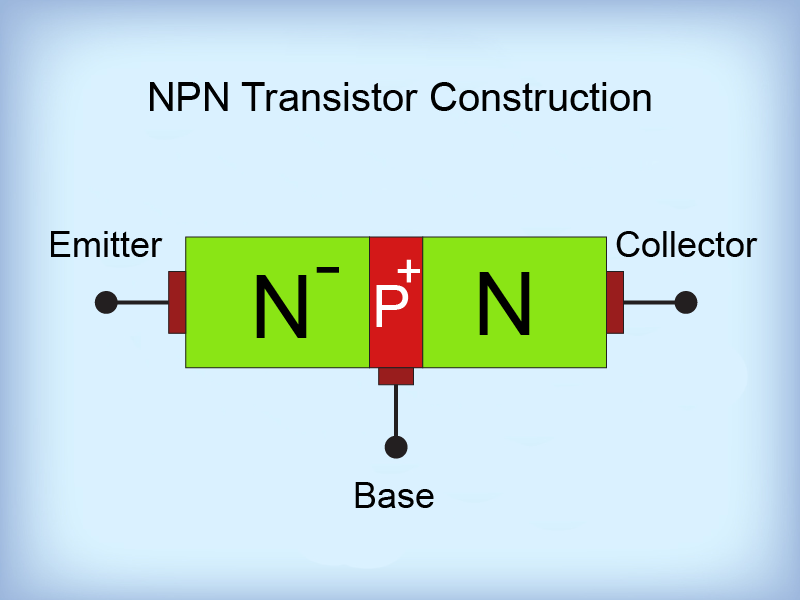
NPN Transistors
This is an NPN transistor. As you can see in this diagram, it is opposite of the PNP transistor. The P-type silicon (the red layer) is sandwiched between two N-type materials (the green layers). The NPN configuration is the most commonly used transistor.
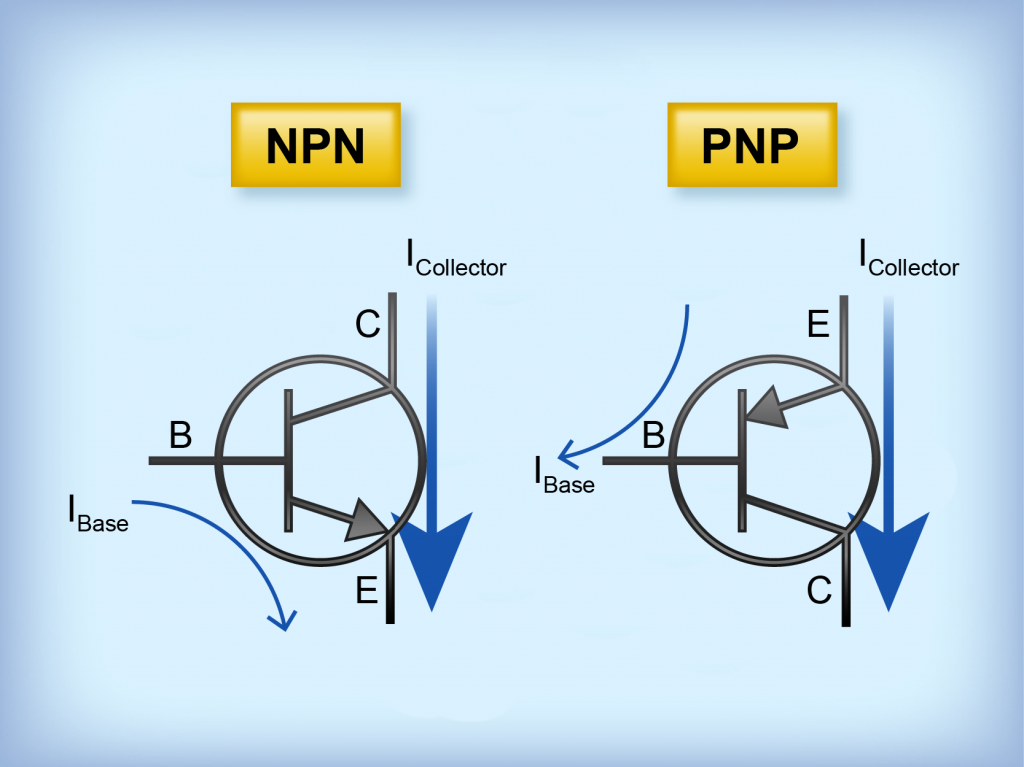
The schematic symbols show the three terminals of the transistor. If the arrow of the schematic symbol points outward, the transistor is an NPN transistor. If the arrow points inward, the transistor is a PNP transistor.
For in depth information about bipolar transistors, including common calculations and biasing techniques, visit the TTS wiki page under the heading Bipolar Transistors Fundamentals. TTS is your source for all things maintenance and operations, contact one of our Process Improvement Specialists for more information about our services.

